Calcular área del círculo
Calcular área del círculo
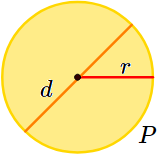
$$ \text{Área } = r^2 \cdot \pi$$
- Calculadora online que muestra las operaciones
- Fórmulas que utiliza la calculadora
- Problemas resueltos sobre el área del círculo
●◆⬟ Calculadora del área
Rellenar únicamente un hueco y presionar el botón CALCULAR. Las operaciones se muestran debajo.
| Radio: | \(r\) = | |
| Diámetro: | \(d\) = | |
| Perímetro: | \(P\) = | |
| Lado cuadrado inscrito: | \(L\) = | |
| Área | \(A\) = |
●◆⬟ Fórmulas
- \(r\) es el radio: distancia del centro del círculo a cualquier punto de la circunferencia (borde del círculo)
- \(d\) es el diámetro: longitud del segmento que une dos puntos de la circunferencia y que pasa por su centro. Es igual a 2 veces el radio: \( d = 2\cdot r\).
- \(P\) es el perímetro: longitud de la circunferencia (borde del círculo). Es igual a 2 veces el radio por \(\pi\): \( P = 2\cdot \pi \cdot r\).
Área
\(A = \pi r^2\)
\(A = \frac{d^2}{4} \)
\(A = \frac{P^2}{4\pi} \)
\(A = \frac{\pi L^2}{2}\)
Radio
\(r = \frac{d}{2}\)
\(r = \frac{P}{2\pi}\)
\(r = \sqrt{\frac{A}{\pi}}\)
\(r = \frac{L}{\sqrt{2}}\)
Diámetro
\(d = 2r\)
\(d = \frac{P}{\pi}\)
\(d = 2\sqrt{\frac{A}{\pi}}\)
\(d = L\sqrt{2}\)
Perímetro
\(P = 2r\pi\)
\(P = d\pi\)
\(P = 2\sqrt{A\pi}\)
\(P = L\pi \sqrt{2}\)
Lado cuadrado inscrito
\(L = r\sqrt{2}\)
\(L = \frac{2}{\sqrt{2}}\)
\(L = \sqrt{\frac{2A}{\pi}}\)
\(L = \frac{P}{\pi \sqrt{2}}\)
●◆⬟ Problemas resueltos
A continuación, resolvemos algunos problemas teóricos relacionados con el área del círculo.
Problema 1
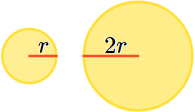
¿El área del círculo de radio \(2r\) es el doble que el área del círculo de radio \(r\)?
Solución:
El problema nos pregunta si el área del círculo sería el doble si multiplicamos por 2 su radio. La respuesta es negativa porque, por ejemplo, el área del círculo de radio 1 es \(\pi\), mientras que el área del círculo de radio \(2\) es \(4\pi\).
Vamos a ver que, en efecto, el área se cuadruplica al doblar el radio.
El área del círculo de radio \(r\) es
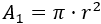
El área del círculo de radio \(2r\) es
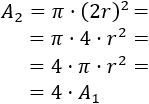
Es decir, el área del círculo cuyo radio es \(2r\) es exactamente el cuádruple del área del círculo de radio \(r\):
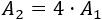
Problema 2
Hay un círculo determinado cuyo valor numérico del área, \(A\), coincide con el valor numérico de su perímetro, \(P\). Calcula el radio de dicho círculo.
Solución:
El problema nos pregunta que calculemos el radio \(r\) para que \(A = P\).
La fórmula del área es
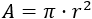
La fórmula del perímetro es
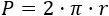
Queremos que el área y el perímetro sean iguales, así que igualamos las fórmulas:
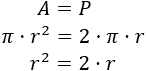
En la última línea hemos cancelado el número \(\pi\) por estar en ambos lados de la igualdad. Matemáticamente, no podemos hacer lo mismo con el radio porque es una incógnita. Debemos calcular \(r\) como una ecuación incompleta de segundo grado:
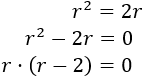
La ecuación tiene dos soluciones: \(r = 0\) y \(r = 2\). La primera no nos sirve ya que el círculo de radio \(0\) es un punto (y no un círculo).
Por tanto, el círculo buscado es el que tiene radio \(r = 2\) y su área y perímetro son
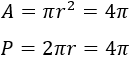
Observación: El problema se refiere al valor numérico puesto que el área son unidades al cuadrado. Así, si el radio son \(2\text{ cm}\), el área del círculo es \(4\pi \text{ cm}^2\) y el perímetro es \(4\pi\text{ cm}\).
Problema 3
Calcula el radio \(r\) del único círculo cuyo valor numérico del área coincide con el de su diámetro.
Solución:
Del mismo modo que hicimos con el problema anterior, igualamos las fórmulas del área y del diámetro y resolvemos la ecuación:
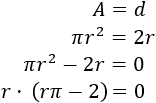
Una de las soluciones es \(r = 0\), que no nos sirve. La otra es

En efecto, el área y el diámetro del círculo de radio \(r = 2/\pi\) son

Problema 4
Obtén la fórmula para calcular el área del círculo en función del diámetro \(d\) y la fórmula para calcular el diámetro en función del área.
Solución:
Por un lado, sabemos la fórmula del área del círculo de radio \(r\):
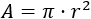
Por otro lado, sabemos que el diámetro del circulo de radio \(r\) es
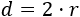
De esta fórmula obtenemos el radio \(r\):
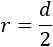
Ahora, sustituimos esta fórmula en la del área:

Por tanto, la primera fórmula buscada es
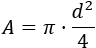
De esta misma fórmula podemos obtener el diámetro a partir del área:
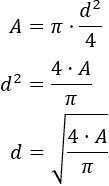
Por tanto, la otra fórmula es
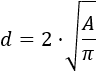
Problema 5
Obtener una fórmula para calcular el área del círculo a partir del lado del cuadrado inscrito y viceversa.
Solución:
Observemos que la diagonal del cuadrado coincide con el diámetro del círculo:
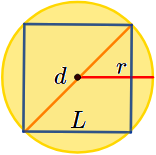
Observemos también que el diámetro del círculo divide en cuadrado en dos triángulos rectángulos de hipotenusa \(d\) y catetos \(L\). Por tanto, podemos aplicar el teorema de Pitágoras a uno de dichos triángulos rectángulos para obtener una fórmula para calcular el diámetro \(d\) en función del lado \(L\):
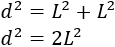
Recordemos que anteriormente obtuvimos la fórmula del área del círculo en función de su diámetro \(d\):
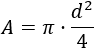
Sustituyendo \(d^2\) en la fórmula anterior tenemos:
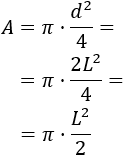
Por tanto, la fórmula para el área del círculo a partir del lado del cuadrado inscrito es
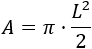
De esta misma fórmula podemos obtener el lado del cuadrado a partir del área del círculo:
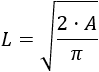
●◆⬟ Calcularea.com
Calcularea: calculadoras de áreas ©