Calcular área del cuadrado
Calcular área del cuadrado
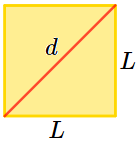
$$ \text{Área } = L^2$$
- Calculadora online que muestra las operaciones
- Fórmulas que utiliza la calculadora
- Problemas resueltos sobre el área del cuadrado
●◆⬟ Calculadora del área
Rellenar únicamente un hueco y presionar el botón CALCULAR. Las operaciones se muestran debajo.
| Lado: | \(L\) = | |
| Perímetro: | \(P\) = | |
| Diagonal: | \(d\) = | |
| Área | \(A\) = |
●◆⬟ Fórmulas
- \(L\) es el lado: la base o la altura del cuadrado, que coinciden.
- \(P\) es el perímetro: la suma de los lados del cuadrado, lo que mide su borde.
- \(d\) es la diagonal: la distancia entre dos vértices no consecutivos (divide el cuadrado en dos triángulos rectángulos).
Área
\( A = L^2 \)
\( A = \frac{P^2}{16}\)
\( A = \frac{d^2}{2}\)
Lado
\( L = \sqrt{A}\)
\( L = \frac{P}{4} \)
\( L = \frac{d}{\sqrt{2}} \)
Perímetro
\( P = 4\cdot L\)
\( P = 4\cdot \sqrt{A}\)
\( P = d\cdot \frac{4}{\sqrt{2}}\)
Diagonal
\( d = L\cdot \sqrt{2}\)
\( d = P\cdot \frac{\sqrt{2}}{4} \)
\( d = \sqrt{2\cdot A}\)
●◆⬟ Problemas resueltos
A continuación, resolvemos algunos problemas teóricos relacionados con el área del cuadrado.
Problema 1
Hallar el lado, \(L\), de un cuadrado para que el valor numérico de su área, \(A\), coincida con el de su perímetro, \(P\).
Solución:
La fórmula del área del cuadrado de lado \(L\) es
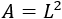
La fórmula del perímetro del cuadrado de lado \(L\) es
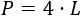
Como queremos que el área y el perímetro coincidan, igualamos ambas fórmulas y resolvemos la ecuación de segundo grado incompleta resultante:
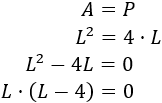
Una de las soluciones de la ecuación anterior es \(L = 0\), que no nos sirve ya que no podemos considerar el cuadrado de lado 0. La otra solución es \(L = 4\).
Por tanto, el valor numérico del área y del perímetro del cuadrado coinciden cuando su lado mide 4.
En efecto, el área y el perímetro de dicho cuadrado son
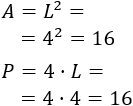
Problema 2
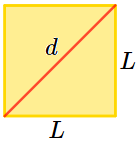
Hallar el lado, \(L\), de un cuadrado para que el valor numérico de su área, \(A\), coincida con el de su diagonal, \(d\).
Solución:
La fórmula del área del cuadrado de lado \(L\) es
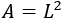
Observad que la diagonal del cuadrado lo divide en dos triángulos rectángulos de hipotenusa \(d\) y catetos \(L\):
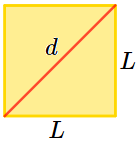
Podemos calcular \(d\) aplicando el teorema de Pitágoras:
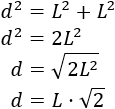
Por tanto, la fórmula del diámetro del cuadrado de lado \(L\) es
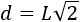
Como queremos que el área y la diagonal coincidan, igualamos ambas fórmulas y resolvemos la ecuación de segundo grado incompleta resultante:
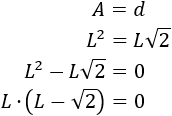
Una de las soluciones de la ecuación anterior es \(L = 0\), que no nos sirve ya que no podemos considerar el cuadrado de lado 0. La otra solución es \(L = \sqrt{2}\).
Por tanto, el valor numérico del área y del perímetro del cuadrado coinciden cuando su lado mide \(\sqrt{2}\).
En efecto, el área y la diagonal de dicho cuadrado son
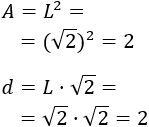
Problema 3
Obtener la fórmula para calcular el área \(A\) de un cuadrado a partir de la longitud de su diagonal \(d\) y viceversa.
Solución:
En el problema anterior obtuvimos una fórmula para calcular la diagonal del cuadrado a partir de su lado:
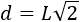
De esta fórmula podemos obtener el lado \(L\) a partir de la diagonal:
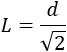
Ahora, sustituimos en la fórmula del área del cuadrado:
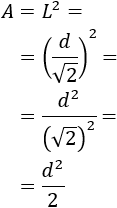
Por tanto, la fórmula para calcular el área a partir de la diagonal es
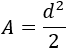
Operamos para aislar la diagonal:
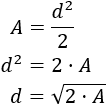
Por tanto, la fórmula para calcular la diagonal a partir del área del cuadrado es
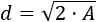
Problema 4
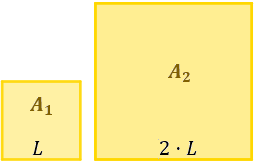
Si se duplica el lado de un cuadrado, ¿se duplica también su área? ¿Qué ocurre con su perímetro?
Solución:
El área del cuadrado de lado \(L\) es
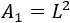
Por tanto, el área del cuadrado de lado \(2\cdot L\) es
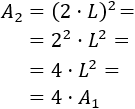
Esto quiere decir que el área del cuadrado se cuadruplica cuando se duplica su lado:
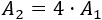
Por otro lado, el perímetro del cuadrado de lado \(L\) es
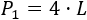
Calculamos el perímetro del cuadrado de lado \(2\cdot L\):
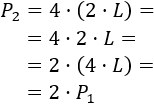
Esto quiere decir que el perímetro del cuadrado se duplica cuando se duplica su lado.
Problema 5

Se tiene un círculo de radio \(r\). Hallar el lado, \(L\), de un cuadrado para que su área coincida con el área del círculo.
Solución:
El área del círculo de radio \(r\) es
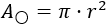
El área del cuadrado de lado \(L\) es
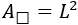
Como queremos que las áreas coincidan, igualamos las fórmulas:
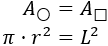
Calculamos \(L\):
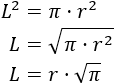
Por tanto, el cuadrado de lado \(L = r\cdot \sqrt{\pi}\) tiene el mismo área que el círculo de radio \(r\).
●◆⬟ Calcularea.com
Calcularea: calculadoras de áreas ©