Calcular área del rectángulo
Calcular área del rectángulo
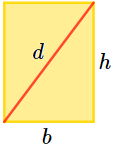
$$ \text{Área } = b \cdot h$$
- Calculadora online que muestra las operaciones
- Fórmulas que utiliza la calculadora
- Problemas resueltos sobre el área del rectángulo
●◆⬟ Calculadora del área
Rellenar únicamente 2 huecos y presionar el botón CALCULAR. Las operaciones se muestran debajo.
| Base: | \(b\) = | |
| Altura: | \(h\) = | |
| Perímetro: | \(P\) = | |
| Diagonal: | \(d\) = | |
| Área | \(A\) = |
Nota: los datos de la base (b) y la altura (h) son intercambiables, ya que intercambiarlos no afecta a las fórmulas.
●◆⬟ Fórmulas
- \(b\) es la base y \(h\) es la altura (son los lados del rectángulo): hay dos bases y dos alturas. La base y la altura son perpendiculares entre sí.
- \(d\) es la diagonal: une dos vértices no consecutivos del rectángulo. Hay dos diagonales que dividen el rectángulo en dos triángulos rectángulos.
- \(P\) es el perímetro (suma de los lados) y \(A\) es el área.
Área
\( A = b\cdot h \)
\(A = \frac{h}{2}\cdot (P-2h) \)
\(A = h\cdot \sqrt{d^2 - h^2} \)
\(A = \frac{P^2 – 4d^2}{8} \)
Perímetro
\(P = 2b + 2h \)
\(P = 2h + 2\sqrt{d^2 -h^2 } \)
\(P = 2\left( h + \frac{A}{h}\right)\)
\(P = \sqrt{4d^2 + 8A} \)
Diagonal
\(d = \sqrt{b^2 + h^2} \)
\(d = \frac{1}{2}\sqrt{4h^2 + (P-2h)^2} \)
\(d = \sqrt{h^2 + \frac{A^2}{h^2}} \)
\(d = \frac{\sqrt{P^2-8A}}{2} \)
Base (o altura)
\(b = \frac{A}{h}\)
\(b = \frac{P - 2h}{2} \)
\(b = \frac{P}{4} \pm \frac{\sqrt{8d^2 – p^2}}{4} \)
\(b = \frac{P}{4} \pm \frac{\sqrt{P^2-16A}}{-4} \)
\(b = \sqrt{\frac{d^2 \pm \sqrt{d^4-4A^2}}{2}} \)
\(b = \sqrt{d^2 - h^2}\)
●◆⬟ Problemas resueltos
A continuación, resolvemos algunos problemas teóricos relacionados con el área del rectángulo.
Problema 1

Hallar el área y el perímetro de un rectángulo de base 3 cm y altura 6 cm.
Solución:
La base y la altura son
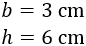
El perímetro es la suma de los cuatro lados:
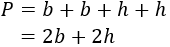
Calculamos el perímetro:
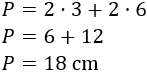
El área es la base por la altura:
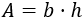
Calculamos el área:
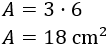
Nota: es importante no olvidar que el perímetro es en \(\text{cm}\) y el área es en \(\text{cm}^2\).
Problema 2
¿Cuánto mide la diagonal de un rectángulo de base \(b\) y altura \(h\)? Hallar dos fórmulas para calcular la base y la altura a partir de la diagonal.
Solución:
Representamos un rectángulo de base \(b\) y altura \(h\) con diagonal \(d\):
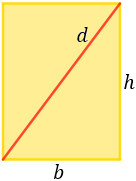
La diagonal es el segmento que une dos vértices no consecutivos del rectángulo. Un rectángulo tiene 2 diagonales y miden lo mismo:
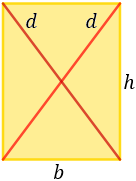
La diagonal divide el rectángulo en un triángulo rectángulo, lo que permite calcular su longitud mediante el teorema de Pitágoras:
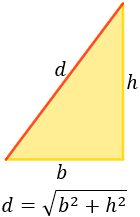
De esta fórmula podemos obtener 2 fórmulas: una para calcular la base y otra para calcular el área.
Elevamos al cuadrado ambos lados:
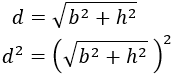
El signo de la raíz desaparece al elevar al cuadrado:
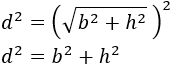
Aislamos la base:
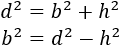
Hacemos la raíz cuadrada:
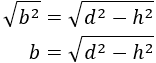
Por tanto, la base a partir de la diagonal (y de la altura) es
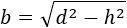
Siguiendo los pasos anteriores, la altura a partir de la diagonal (y la base) es
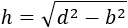
Problema 3
Hallar la relación que debe haber entre la base y la altura de un rectángulo para que el valor numérico de su perímetro coincida con el de su área (tal y como ocurre con el rectángulo del Problema 1).
Proporcionar 3 ejemplos de estos rectángulos.
Solución:
La fórmula del área es base \(b\) por altura \(h\):
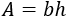
La fórmula del perímetro es
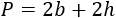
Queremos que el área y el perímetro sean iguales:
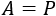
Por tanto, tenemos
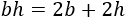
Aislamos la \(b\) en un lado:
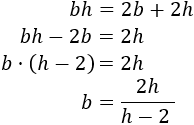
Luego la relación que debe haber entre base y altura es
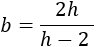
Para tener 3 ejemplos sólo tenemos que dar a \(h\) tres valores distintos:
-
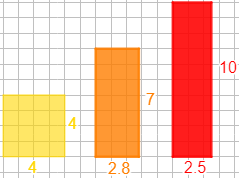
Si \(h=4\), entonces la base debe ser
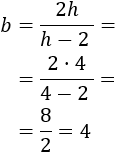
Rectángulo de base 4 y altura 4 (es un cuadrado).
-
Si \(h=7\), entonces la base debe ser
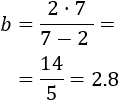
Rectángulo de base 2.8 y altura 7.
-
Si \(h=10\), entonces la base debe ser
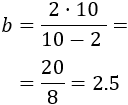
Rectángulo de base 2.5 y altura 10.
Representaciones:
Problema 4
Hallar una fórmula para obtener el área de un rectángulo a partir de su perímetro \(P\) y su diagonal \(d\).
Solución:
Sabemos que las fórmulas del perímetro, del área y de la diagonal son:
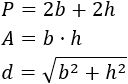
Calculamos el cuadrado del perímetro:
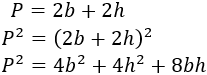
Nota: hemos usado una fórmula para calcular el cuadrado de la suma.
Podemos escribir \(A\) en lugar de \(bh\):
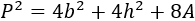
Operamos un poco más:
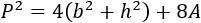
Observad que en la fórmula anterior tenemos el cuadrado de la diagonal (entre paréntesis):
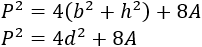
De donde obtenemos la fórmula para el área:
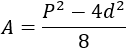
Problema 5 (difícil)
Hallar una fórmula para calcular la base \(b\) y la altura \(h\) de un rectángulo a partir de su perímetro \(P\) y su diagonal \(d\).
Solución:
Sabemos que las fórmulas del perímetro y de la diagonal son:
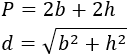
Aislamos la altura en la fórmula del perímetro:
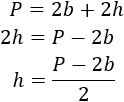
Aislamos la altura en la fórmula de la diagonal:
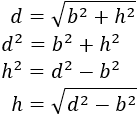
Igualamos las dos expresiones obtenidas (porque \(h = h\)):
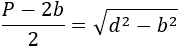
Ahora vamos a trabajar en la identidad anterior: elevaremos al cuadrado y operaremos hasta obtener la forma de una ecuación de segundo grado completa para aplicar la fórmula de estas ecuaciones:
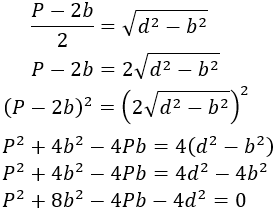
Observemos que tenemos la forma de una ecuación de segundo grado completa cuya incógnita es \(b\):
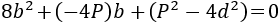
Los coeficientes de la ecuación son
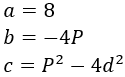
Recordemos que la fórmula de las ecuaciones de segundo grado con la forma \(ax^2 + bx + c = 0\) es
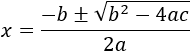
Nota: no hay que confundir la \(b\) de la fórmula anterior con la \(b\) de la base de nuestro rectángulo.
Aplicamos la fórmula a nuestra ecuación:

Operando un poco, obtenemos que
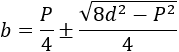
Sustituyendo en una de las fórmulas iniciales, tendremos \(h\):
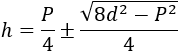
Es decir, que uno de los lados del rectángulo es
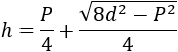
Y el otro lado es
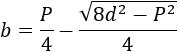
Nota: que llamemos \(h\) ó \(b\) a uno u otro lado del rectángulo no nos importa.
Problema 6 (muy difícil)
Hallar una fórmula para calcular la base \(b\) y la altura \(h\) de un rectángulo a partir de su área \(A\) y su diagonal \(d\).
Solución:
Sabemos que las fórmulas del área y de la diagonal son:
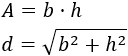
De la fórmula del área podemos calcular \(h^2\):
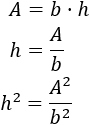
De la fórmula de la diagonal podemos aislar \(b^2\):
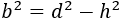
Podemos sustituir en esta fórmula la \(h^2\) obtenida a partir del área:
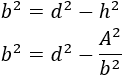
Operando un poco, obtenemos una ecuación bicuadrada:
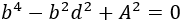
Podemos resolver esta ecuación fácilmente realizando un cambio de variable \(t = b^2\). Finalmente, al deshacer el cambio, obtendremos la solución que buscamos:
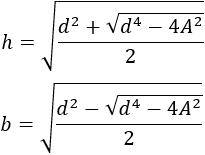
Nota: al igual que en el problema anterior, que llamemos \(h\) ó \(b\) a uno u otro lado del rectángulo es indiferente.
●◆⬟ Calcularea.com
Calcularea: calculadoras de áreas ©