Calcular área del rombo
Calcular área del rombo
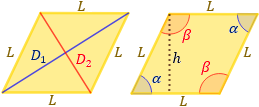
$$ \begin{array}{rcl} \text{Área:} & A = & \frac{D_1\cdot D_2}{2} \\ \text{Área:} & A = & L\cdot h \\ \text{Área:} & A = & L^2\cdot \sin(\alpha )\end{array} $$
- Calculadora online que muestra las operaciones
- Fórmulas que utiliza la calculadora
- Problemas resueltos sobre el área del rombo
●◆⬟ Calculadora del área
Rellenar únicamente 2 huecos y presionar el botón CALCULAR. Las operaciones se muestran debajo.
Nota: si se proporciona una diagonal y un ángulo, ha de tenerse en cuenta que α es el ángulo que corta D₁ y β es el que corta D₂ (véase la representación).

|
||
| Diagonal 1: | \(D_1\) = | |
| Diagonal 2: | \(D_2\) = | |
| Altura: | \(h\) = | |
| Lado: | \(L\) = | |
| Ángulo 1: | \(\alpha \) = | \(^{\circ}\) |
| Ángulo 2: | \(\beta \) = | \(^{\circ}\) |
| Área | \(A\) = | |
●◆⬟ Fórmulas
- \(D_1\) y \(D_2\) son las diagonales: unen vértices no contiguos.
- \(\alpha\) y \(\beta\) son los ángulos interiores: hay 4 y son iguales 2 a 2. Todos ellos suman 360 grados.
- \(L\) es el lado: hay 4 lados y miden lo mismo.
- \(h\) es la altura: distancia entre lados opuestos.
Altura
\( h = \frac{D_1\cdot D_2 }{\sqrt{D_1^2+D_2^2}}\)
\( h = \frac{2AD_i}{\sqrt{D_i^4 + 4A^2}} \)
\(h = \frac{A}{L} \)
Ángulos
\( \alpha = \arcsin\left( \frac{A}{L^2}\right) \)
\( \beta = 180^{\circ} - \alpha\)
Diagonales
\( D_j = \frac{h\cdot D_i}{\sqrt{D_i^2-h^2}} \)
\( D_j = \sqrt{4L^2 – D_i^2} \)
\(D_{i,j} = \sqrt{2L^2 \pm 2\sqrt{L^4 -A^2}} \)
Área
\( A = \frac{D_1\cdot D_2}{2}\)
\( A = h\cdot L\)
\( A = L^2 \cdot \sin(\alpha)\)
\( A = L^2 \cdot \sin(\beta)\)
\( A =^* D_2^2\cdot \frac{1+cos(\beta)}{2\sin(\beta)} \)
\( A =^* D_1^2\cdot \frac{1+cos(\alpha)}{2\sin(\alpha)} \)
Lado
\( L = \frac{\sqrt{D_1^2+D_2^2}}{2} \)
\( L = \frac{\sqrt{D_i^4 + 4A^2}}{2D_i} \)
\( L = \frac{A}{h}\)
\( L = \frac{h}{ \sin(\alpha )} \)
\( L = \sqrt{\frac{A}{\sin(\alpha )}} \)
●◆⬟ Problemas resueltos
A continuación, resolvemos algunos problemas relacionados con el área del rombo.
Problema 1
¿Sabrías decir por qué la fórmula del área de un rombo con diagonales \(D_1\) y \(D_2\) es la siguiente?
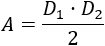
Solución:
Representamos un rombo con diagonales \(D_1\) y \(D_2\) y segmentos paralelos a dichas diagonales para formar un rectángulo:
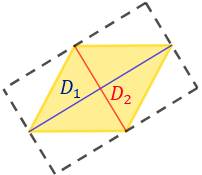
El área del rectángulo obtenido tiene base \(D_1\) y altura \(D_2\), por lo que su área es
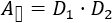
Es fácil ver que el área del rombo es la mitad del área del rectángulo, así que el área del rombo es el semiproducto de sus diagonales:
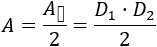
Problema 2
¿Sabrías decir por qué la fórmula del área de un rombo de lado \(L\) y altura \(h\) es la siguiente?
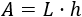
Solución:
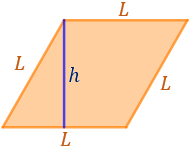
Representamos el rombo con su altura:
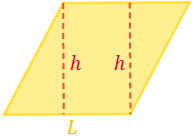
En el rombo se puede ver un rectángulo y dos triángulos. Cortamos por la altura para unir uno de los triángulos al otro:
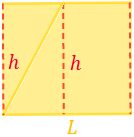
El área del rectángulo construido de base \(L\) y altura \(h\) es
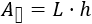
El área del rombo es la misma que la del rectángulo porque lo hemos construido a partir del propio rombo, sin cambiar su área, solo su forma.
Problema 3
Hallar una fórmula para calcular el lado \(L\) de un rombo a partir de sus diagonales \(D_1\) y \(D_2\).
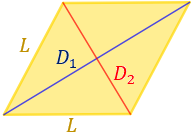
Solución:
Si cortamos el rombo por las diagonales, obtenemos cuatro triángulos rectángulos de hipotenusa \(L\) y catetos \(D_1/2\) y \(D_2/2\):
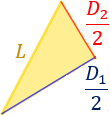
Podemos aplicar el teorema de Pitágoras:
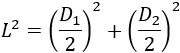
Operamos:
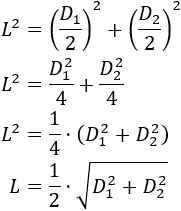
Por tanto, la fórmula para el lado es
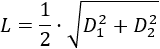
Problema 4
Hallar una fórmula para calcular la altura \(h\) de un rombo de diagonales \(D_1\) y \(D_2\).
Solución:
Tenemos dos fórmulas para el área del rombo:
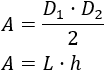
Podemos igualarlas:
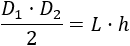
Cambiamos \(L\) por la fórmula obtenida en el problema anterior:
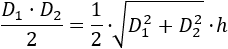
Operamos y aislamos \(h\):
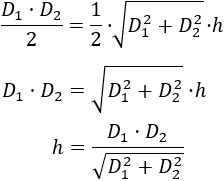
Por tanto, la fórmula buscada es
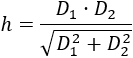
Problema 5
Hallar una fórmula para calcular los ángulos interiores \(\alpha\) y \(\beta\) de un rombo sabiendo que sus lados miden \(L\) y su área es \(A\).
Solución:
El área del rombo es
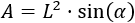
Así que, por un lado, tenemos
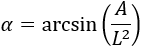
Por otro lado, como la suma de los ángulos interiores del rombo debe ser 360 grados,
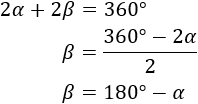
Con lo que
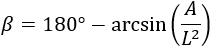
Problema 6 (difícil)
Hallar una fórmula para calcular las diagonales \(D_1\) y \(D_2\) de un rombo sabiendo que sus lados miden \(L\) y su área es \(A\).
Solución:
La fórmula del área a partir de las diagonales es
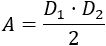
Aislamos una diagonal:
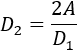
Recordemos la fórmula obtenida en el problema 3:
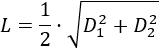
Elevamos al cuadrado:
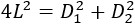
Sustituimos \(D_2\) por la expresión obtenida anteriormente:
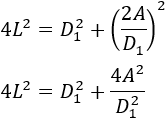
Operando, obtenemos una ecuación bicuadrada:
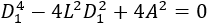
De donde obtenemos
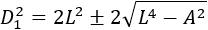
Y ahora, tomando raíces, tenemos
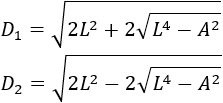
●◆⬟ Calcularea.com
Calcularea: calculadoras de áreas ©