Calcular área del triángulo
Calcular área del triángulo
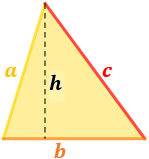
$$ \begin{array}{rcl} \text{Área:} & A = & \frac{b \cdot h}{2} \\ \text{Área:} & A = & \sqrt{s(s-a)(s-b)(s-c)} \\ \text{Semiperímetro:} & s = & \frac{a+b+c}{2}\end{array} $$
- 4 calculadoras online que muestran las operaciones
- Calculadora 1: a partir de la base y la altura.
- Calculadora 2: a partir de los lados.
- Calculadora 3: triángulo equilátero: a partir del lado o de la altura.
- Calculadora 4: triángulo isósceles: a partir de los lados o de un lado y la altura.
- Fórmulas que utiliza la calculadora
- Problemas resueltos sobre el área del triángulo
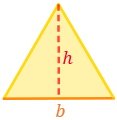
●◆⬟ Calculadora 1 (área, base y altura)
Rellenar únicamente 2 huecos y presionar el botón CALCULAR. Las operaciones se muestran debajo.
 |
||
| Base: | \(b\) = | |
| Altura: | \(h\) = | |
| Área | \(A\) = | |
Fórmulas que usa la calculadora:
\( A = \frac{b\cdot h}{2} \)
\(b = \frac{2\cdot A}{h} \)
\(h = \frac{2\cdot A}{b} \)
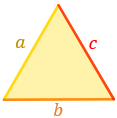
●◆⬟ Calculadora 2 (lados)
Rellenar únicamente 3 huecos y presionar el botón CALCULAR. Las operaciones se muestran debajo.
 |
||
| Lado a: | \(a\) = | |
| Lado b: | \(b\) = | |
| Lado c: | \(c\) = | |
| Área | \(A\) = | |
Fórmulas que usa la calculadora:
\( s = \frac{a+b+c}{2} \)
\(A = \sqrt{s\cdot (s-a) \cdot (s-b)\cdot (s-c)} \)
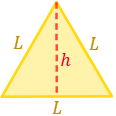
●◆⬟ Calculadora 3 (triángulo equilatero)
Rellenar únicamente 1 hueco y presionar el botón CALCULAR. Las operaciones se muestran debajo.
 |
||
| Lado: | \(L\) = | |
| Altura: | \(h\) = | |
| Área | \(A\) = | |
Fórmulas que usa la calculadora:
\(A = \frac{L^2\cdot \sqrt{3}}{4}\)
\(A = \frac{h^2}{\sqrt{3}}\)
\(L = \frac{2\cdot h}{\sqrt{3}}\)
\(L = 2\sqrt{\frac{A}{\sqrt{3}}}\)
\(h = \sqrt{A\cdot \sqrt{3}}\)
\( h = \frac{\sqrt{3}}{2}\cdot L \)
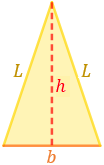
●◆⬟ Calculadora 4 (triángulo isósceles)
Rellenar únicamente 2 huecos y presionar el botón CALCULAR. Las operaciones se muestran debajo.
 |
||
| Lado: | \(L\) = | |
| Base: | \(b\) = | |
| Altura: | \(h\) = | |
| Área | \(A\) = | |
Fórmulas que usa la calculadora:
\(A = \frac{b}{4}\sqrt{4L^2 - b^2}\)
\( A = h\sqrt{L^2 - h^2}\)
\( A = \frac{b\cdot h}{2}\)
\(L =\frac{1}{2b}\cdot \sqrt{16A^2+b^4} \)
\( L = \frac{1}{h}\cdot \sqrt{A^2+h^4} \)
\(L =\frac{1}{2}\cdot \sqrt{4h^2+b^2} \)
\(b = 2\sqrt{L^2-h^2} \)
\(b = \sqrt{ 2L^2 -2\sqrt{L^4 -4A^2} } \)
\( b=\frac{2A}{h}\)
\(h = \frac{1}{2}\sqrt{4L^2 - b^2}\)
\( h = \frac{1}{2} \sqrt{2L^2 +2\sqrt{L^4 -4A^2} } \)
\( h = \frac{2A}{b} \)
●◆⬟ Problemas resueltos
A continuación, resolvemos algunos problemas relacionados con el área del triángulo.
Problema 1
Hallar el área de los siguientes triángulos de base 3 cm y altura 6 cm:
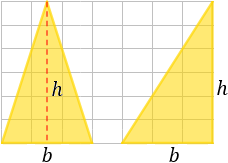
Solución:
Aplicamos la fórmula que utiliza la base (b) y la altura (h):
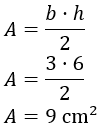
Luego el área de cada uno de los dos triángulos es \(9\text{ cm}^2\).
Se trata de dos triángulos cuyas bases y alturas miden los mismo, por lo que tienen la misma área. Sin embargo, los otros lados no miden lo mismo.
El triángulo de la izquierda es isósceles (dos lados iguales) y el de la derecha es escaleno rectángulo (lados distintos y un ángulo recto).
Problema 2
¿Cuál es el área del triángulo equilátero de lado 2 cm?
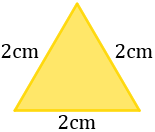
Solución:
Como el triángulo es equilátero, todos sus lados miden lo mismo: 2 cm.
Es más fácil aplicar la fórmula que usa el semiperímetro (fórmula de Herón) que calcular la altura:
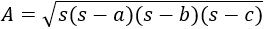
donde
- \(s\) es el semiperímetro (la mitad del perímetro) y
- \(a\), \(b\) y \(c\) son los lados del triángulo.
Calculamos el semiperímetro:
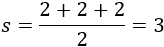
Como los lados miden lo mismo, las diferencias de la fórmula dan el mismo resultado:
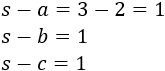
Aplicamos la fórmula de Herón:
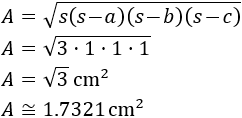
Problema 3
¿Puede existir un triángulo cuyos lados midan 1, 1 y 2 centímetros? ¿Cuál sería su área?
Solución:
Si solo 2 lados de un triángulo miden lo mismo, entonces se trata de un triángulo isósceles:
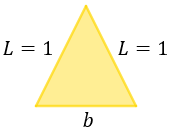
La altura \(h\) divide el triángulo en 2 triángulos rectángulos iguales:
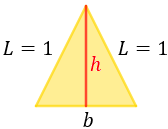
Aplicamos el teorema de Pitágoras:
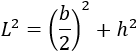
Sabemos que \(L=1\), así que
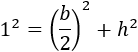
Ahora supongamos que \(b=2\), porque \(b\) es el otro lado y se supone que mide 2 centímetros. Entonces, tendríamos
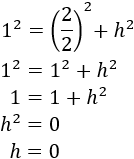
Es evidente que la altura \(h\) no puede ser 0, porque entonces no existiría el triángulo.
En efecto, el semiperímetro del supuesto triángulo sería
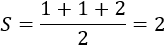
Aplicamos la fórmula de Herón para calcular el área del supuesto triángulo:
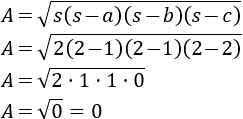
El área del triángulo sería \(0\) (porque no tiene altura y, por tanto, no sería un triángulo).
Problema 4
¿Cuánto deben medir los lados de un triángulo equilátero para que su área sea el doble que el área del triángulo rectángulo de lados \(1\), \(2\) y \(\sqrt{3}\) centímetros?
Ayuda: puede servir la fórmula del problema siguiente para calcular el área de un triángulo equilátero de lado \(L\):
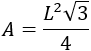
Solución:
Vamos a estudiar cuál de los tres lados es la hipotenusa \(h\) ayudándonos de la fórmula de Pitágoras:
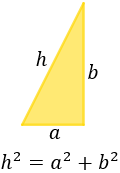
Si la hipotenusa es \(h = 1\), entonces tendríamos una falsedad:
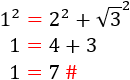
Si la hipotenusa es \(h = \sqrt{3}\), entonces tendríamos una falsedad:
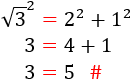
Si la hipotenusa es \(h = 2\), entonces no tenemos ningún problema:
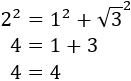
Por tanto, el triángulo del problema es
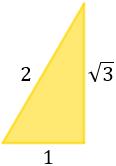
Podemos construir un triángulo equilátero con dos triángulos como el anterior:
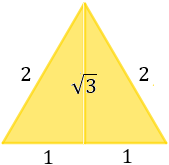
Este triángulo es equilátero porque sus tres lados miden lo mismo. Además, su área es el doble del triángulo del triángulo inicial (porque se usan dos triángulos iguales).
Por tanto, el triángulo buscado en el problema es el triángulo equilátero de lado 2 centímetros.
Otra forma de resolver el problema es usar la fórmula del problema siguiente, que es el área de un triángulo equilátero de lado \(L\):
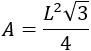
Calculamos el área del triángulo rectángulo de lados \(1\), \(2\) y \(\sqrt{3}\), que sabemos que tiene base \(1\) y altura \(\sqrt{3}\):
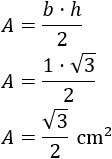
El doble de esta área es
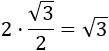
Sustituimos esta área en la fórmula del triángulo equilátero para calcular su lado:
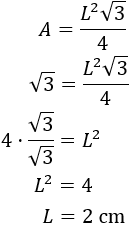
Luego, aplicando la fórmula, el triángulo equilátero cuya área es el doble del buscado es el de lado 2 centímetros, como vimos anteriormente.
Problema 5
Comprobar que el área de un triángulo equilátero de lado \(L\) es
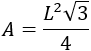
Solución:
Los tres lados de un triángulo equilátero miden lo mismo: \(L\) en nuestro caso.
Podemos calcular el área a partir de la fórmula de Herón:
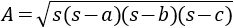
Como \(a = b = c = L\), entonces el semiperímetro del triángulo es
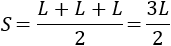
Además,
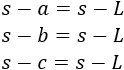
Calculamos \(s-L\) (restando fracciones):
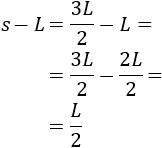
Calculamos el área:
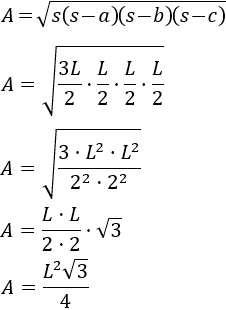
Problema 6
Hallar una fórmula para calcular el área de un triángulo equilátero a partir de su altura \(h\).
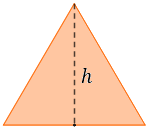
Solución:
La fórmula general del área de un triángulo a partir de su base \(b\) y su altura \(h\) es
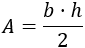
Ahora vamos a buscar una fórmula para calcular la base a partir de la altura y sustituirla en la fórmula anterior. Nos ayudaremos de las propiedades propias de los triángulos equiláteros.
La altura del triángulo equilátero lo divide en dos triángulos rectángulos iguales:
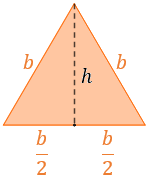
Aplicando el teorema de Pitágoras:
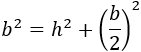
Aislamos la base \(b\):
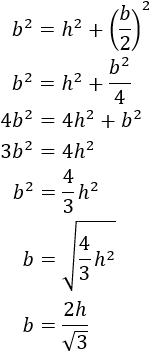
Sustituimos la fórmula obtenida en la del área:
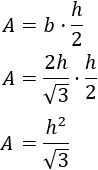
Por tanto, el área de un triángulo equilátero de altura \(h\) es
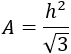
Problema 7
Hallar una fórmula para calcular el área de un triángulo isósceles de lados \(L\) y base \(b\).
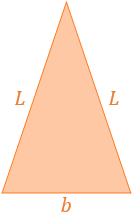
Solución:
La fórmula general del área de un triángulo es
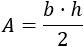
Como desconocemos la altura \(h\), vamos a buscar una fórmula para calcularla.
La altura divide el triángulo en dos triángulos rectángulos:
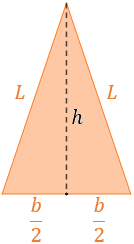
Aplicamos Pitágoras:
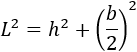
Aislamos la altura \(h\):
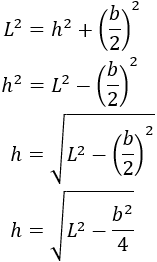
Sustituimos en la fórmula del área:
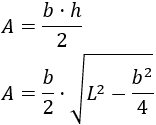
Podemos operar un poco más:
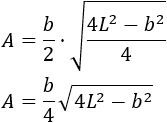
Por tanto, la fórmula del área que buscamos es
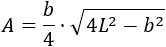
Si en lugar de aislar la \(h\) aislamos la \(b\), obtenemos la fórmula del área a partir de su altura:
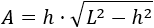
Problema 8
Hallar una fórmula para calcular los lados \(L\) de un triángulo isósceles de lados \(L\) y base \(b\) a partir de su área \(A\) y su base \(b\).
Solución:
En el problema anterior obtuvimos la fórmula para calcular el área a partir de la base \(b\) y el lado \(L\):
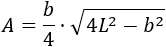
Podemos aislar la \(L\) en la fórmula anterior:
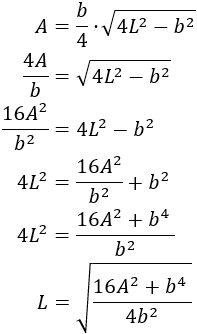
Por tanto, el lado \(L\) en función de el área y de la base es
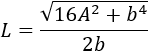
Problema 9
Hallar una fórmula para calcular los lados \(L\) de un triángulo isósceles de lados \(L\) y base \(b\) a partir de su área \(A\) y su altura \(h\).
Solución:
Anteriormente obtuvimos la fórmula para calcular el área a partir de la altura \(h\) y el lado \(L\):
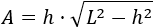
Aislamos \(L\) en la fórmula anterior:
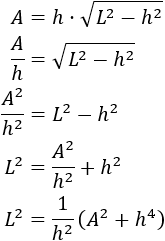
Por tanto, haciendo la raíz cuadrada, tenemos la formula buscada:
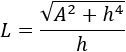
Problema 10
Demostrar la fórmula de Herón para calcular el área de un triángulo de lados \(a\), \(b\) y \(c\), siendo \(s = (a+b+c)/2\) su semiperímetro:
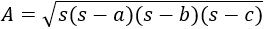
Solución:
Demostración en Herón de Alejandría y la fórmula de Herón.
●◆⬟ Calcularea.com
Calcularea: calculadoras de áreas ©